ベイズ公式メモ

ベイズ統計入門の15-3章を読んでベイズの公式どうやって出てきたかを勉強になったので、それを簡単にまとめるメモ

問題１

目の前にツボが一つあり、AのツボかBのツボであることはわかっているが、見た目ではどちらかわからない。知識として、Aのツボには９個の白球と1個の黒球が入っており、Bのツボには8個の黒球と2個の白球が入っていることを知っている。今、ツボから1個球を取り出したら、黒球だった。目の前のツボはどちらのツボか。

黒球取り出して、Bツボである確率を計算してみると

P(B|黒)  = P(B & 黒) / P(黒) 

= ( P(B) x P(黒|B) ) / P(黒)

= ( P(B) x P(黒|B) ) / ( P(A & 黒) + P(B & 黒))

= ( P(B) x P(黒|B) ) / ( ( P(A) x P(黒|A) ) + ( P(B) x P(黒|B) ) ) 

補足

P(A|B) = P(AとBの重なり) / P(B)

問題２

珍しい病気の診断問題で、仮に千人の中に一人がこの病気にかかるとする。検査ではヒット率が99%で、つまり人が本当に病気にかかって、さらに検査で99%の精度でpositive（病気にかかってる）の結果が出る。逆に病気にかかっていないにも関わらずpositiveの検査結果が出る確率は5%。このようなデータに基づいて一人を選んで、検査して、検査結果はpositiveの場合、この人本当に病気にかかっている確率はどのぐらい。

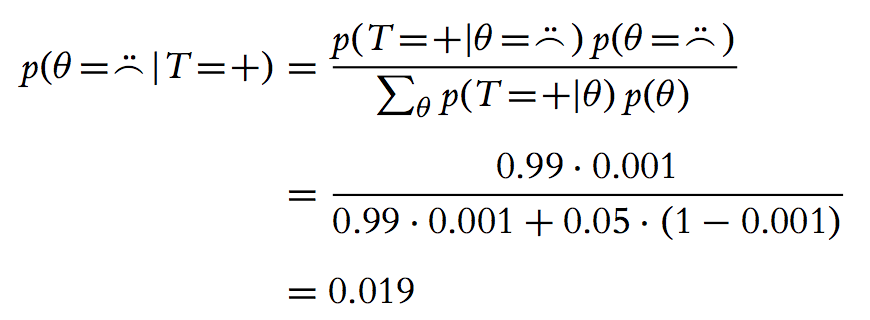
分母は二つの確率の和で、1) 病気かかって、さらにpositiveと診断される確率 2) 病気かかっていないけどpositiveと診断される確率。