TensorflowでLinear Regressionをテストする

2018-09-30 linear regression, tensorflow

Page content

線形回帰は　$Ax= b$ の形でメトリックス方程式で表すことができる。ここで係数$x$を求めたい。 結果は $x = (A^T A)^{-1}A^Tb$

二次元のデータを生成してTensorflowを利用して、問題を解決する。以下ではA.shape = (100, 2), b.shape=(100,1) 最後にx.shape=(2,1)、xの中の要素はslope(傾き)とy intercept(y切片)

import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
sess = tf.Session()

x_vals = np.linspace(0, 10, 100)
# 標準正規乱数 (平均:0.0, 標準偏差:1.0) に従う乱数を 100 件出力
y_vals = x_vals + np.random.normal(0, 1, 100) 


x_vals_column = np.transpose(np.matrix(x_vals))
ones_column = np.transpose(np.matrix(np.repeat(1, 100)))

A = np.column_stack((x_vals_column, ones_column))
b = np.transpose(np.matrix(y_vals))

A_tensor = tf.constant(A)
b_tensor = tf.constant(b)
print("A tensor: {}\nb tensor: {}".format(A_tensor, b_tensor))

$x = (A^T A)^{-1}A^Tb$ を計算する。

tA_A = tf.matmul(tf.transpose(A_tensor), A_tensor)
tA_A_inv= tf.matrix_inverse(tA_A)

product = tf.matmul(tA_A_inv, tf.transpose(A_tensor))
solution = tf.matmul(product, b_tensor)
solution_eval = sess.run(solution)

slope = solution_eval[0][0]
y_intercept = solution_eval[1][0]
print("slope: {}\ny intercept: {}".format(slope, y_intercept))

slope: 0.9737510232298359
y intercept: 0.14039905358306318

best_fit = []
for i in x_vals:
    best_fit.append(slope * i + y_intercept)
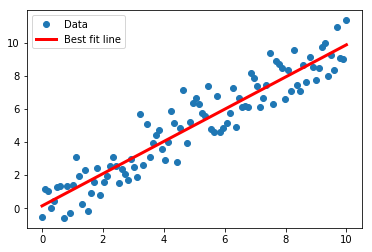
plt.plot(x_vals, y_vals, 'o', label='Data')
plt.plot(x_vals, best_fit, 'r-', label='Best fit line', linewidth=3)
plt.legend(loc=0)

png