逆伝播の仕組み

2018-09-21 math

Page content

やりたいことは簡単のニューラルネットワークの逆伝播の仕組みを計算することです。自分の中の整理のためでもあります。

もっともシンプルの例で、猫なのか、猫じゃないなのかを判断するただ一層のニューラルネットワークで、一枚の画像で訓練するとします。下の図で仕組みを表しています。

png

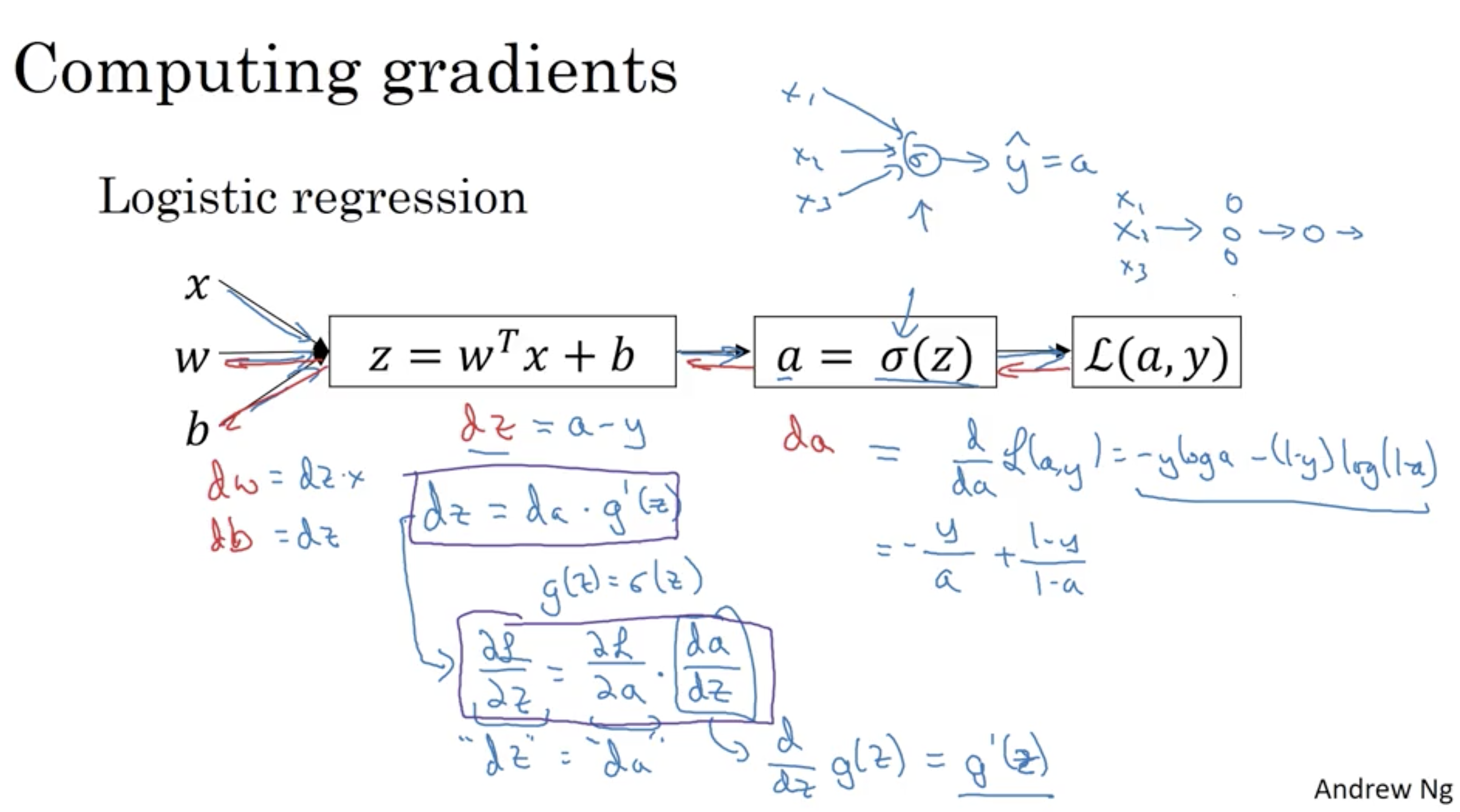
上の図では

$x$ : 入力画像

$w$: 求めたい重み

$b$: 求めたいバイアス

$z$: 順伝播(Forward Propagation)の線形部分

$a$: $z$に対して活性化関数を適した後

$L$: 損失関数(Lost function)

砕けた言い方にするとニューラルネットワークの目的は損失関数を小さくして、その時に重み($w$)とバイアス ($b$) を求めるだけです。

猫であるかどうかを判断する2分類の問題は損失関数として、クロスエントロピー関数(Cross entropy)を使うことができます。下の形になっています。

$L(a, y) = −(ylog(a)+(1−y)log(1−a))$

$a$: 毎回訓練の結果を表しています。0.2, 0.6, 0.9などを値になります。

$y$: 実際ある画像は猫であるかどうかを示す値で、例えば0か1かになります。

$z$に活性関数(Activation Function)を適応する結果は$a$で、活性関数はシグモイド関数の場合、$a = \frac{1}{1+e^{-z}}$ です。

このネットワークの目的は$dW$ (重みの微分)と $db$（バイアスの微分）を求めることで、これらを求めたら下の式で少しずつ重み$W$と$b$を更新して、損失関数の値を小さくします。$\alpha$は学習率(Learning rate)

$W^{[l]} = W^{[l]} - \alpha \text{ } dW^{[l]}$

$b^{[l]} = b^{[l]} - \alpha \text{ } db^{[l]} $

目標がわかったので、これで$dW$を求めてみます。

$dW = \frac{d}{dW}{L(a, y)}$

微分法の中で連鎖律があって、$dW$は下の形に書き換えることができます。

$dW = \frac{dL(a,y)}{da}\frac{da}{dz}\frac{dz}{dW}$

タスクをブレイクダウンして、求めると

$da = \frac{dL(a,y)}{da} = (−(ylog(a)+(1−y)log(1−a)))‘$

$= -y \frac{1}{a} - (1-y) \frac{1}{1-a}(-1)$

$= -\frac{y}{a} + \frac{1-y}{1-a}$

そして$dz$を求める。

$dz = \frac{dL(a,y)}{dz} = \frac{dL(a,y)}{da}\frac{da}{dz}$

$( -\frac{y}{a} + \frac{1-y}{1-a}) (a(1-a)) =$

$a-y$

最後に

$dW = \frac{dL(a,y)}{dW} = \frac{dL(a,y)}{da}\frac{da}{dz}\frac{dz}{dW} =$

$dz*x = (a-y)x$

同じように

$db = \frac{dL(a,y)}{da}\frac{da}{dz}\frac{dz}{db} = dz=(a-y)$

これで全ての未知数はわかったので、重みを更新することができるわけです。

$W^{[l]} = W^{[l]} - \alpha \text{ } dW^{[l]}$

$b^{[l]} = b^{[l]} - \alpha \text{ } db^{[l]} $

このネットワークはもっともシンプルの構造をしているので、そもそも隠れ層もないです。L層ののネットワークになる、求め方は少し複雑になりますが、考え方は一緒で、L層の$dW^{l}$と$db^{l}$を求めるだけです。

実際にこのネットワークを実装する際に上で求めた結果を利用してNumpyで実装する形になります。